Predicting effects of tunnel throttling of annular freeway vehicular flow by a continuum model

Nomenclature

1.   Introduction

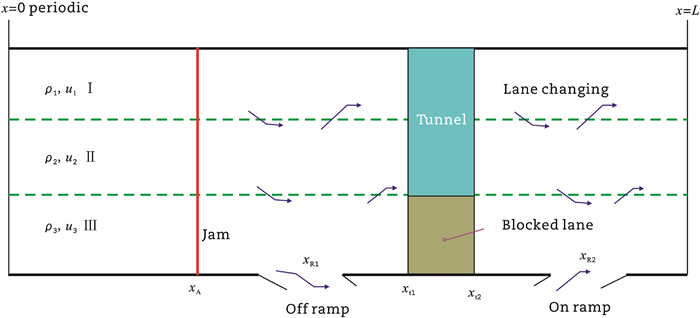
Fluid flow throttling is common in industrial and building service engineering. In transportation science and engineering for vehicular flow, it is renamed as bottleneck. A review of mathematical modeling of vehicular flows indicates that many models have been developed, as reported by Zhang et al. (2018, 2023).

After considerations for macroscopic modeling of multi-lane vehicular flow reported by Michalopoulos et al. (1984), Helbing and Greiner (1997) put forward a macroscopic model of multi-lane traffic flow from a Boltzmann-like gas-kinetic approach. Daganzo (2002) developed a macroscopic behavior theory of traffic dynamics for homogeneous multi-lane freeways. Focusing on the onset of congestion, Pestov et al. (2019) examined the performance of multi-lane freeway traffic on entering road crossings. Smirnova et al. (2014) proposed a multi-lane continuum model, in which an expression of the parameter to describe the acceleration component in the perpendicular direction in relation to lane-changing was derived.

For the studies on bottleneck effects, Goñi-Ros et al. (2016) found that to make reduction of congestion at sags, a highly effective and innovative way is to use cooperative adaptive cruise control systems. Jin (2018) developed a behavioral kinematic wave model for better design and control strategies to enhance the performance of tunnel bottlenecks.

Recently, Li et al. (2023) have investigated freeway tunnel effects on ring road traffic flow by proposing a two-lane traffic model. Huang et al. (2023) have explored the effects on vehicular fuel consumption of a freeway work zone which has a length of 100 m and occupies lanes Ⅲ and Ⅳ by a four-lane model.

The aim of this paper is to predict the effects of tunnel throttling of annular freeway vehicular flow by developing a three-lane continuum model, where the net lane-changing rate between adjacent lanes is described by a vehicular lane-changing time model. The mandatory lane-changing rate from lane Ⅲ to Ⅰ just upstream of the tunnel entrance is described be a random number model, with the random number generated in a small range around a median based on golden section analysis. For vehicular flows on an annular freeway with a tunnel having a length of 2 km, but with just two lanes thus inducing the throttling of vehicular flow. Numerical simulations with a reliable numerical method of 3rd-order accuracy are conducted to provide spatiotemporal evolution of traffic density, and grid traffic speed. The grid traffic speed on different lanes is used to calculate the mean travel time and its fluctuation through each lane. With an artificially-assumed vehicle performance curve relating to vehicle fuel consumption on vehicular speed, both the vehicle fuel consumption through each lane of the annular freeway and the additional vehicle fuel consumption in comparison with the case of lane blockage vanished (LBV) (i.e., the absence of lane blockage or without tunnel throttling) are predicted.

Numerical results reveal that tunnel throttling leads to an earlier traffic jam formation in comparison with the case without tunnel throttling. Under the conditions in this paper, the density threshold of traffic jam formation normalized by jam density is around 0.19, while for the case without tunnel throttling the threshold is 0.22. The ramp effect slightly delays the occurrence of traffic jam, making the threshold become 0.20. The mean travel time for the case without tunnel throttling is slightly longer than that for the case with tunnel throttling. As soon as the tunnel has originated a traffic jam at the tunnel entrance, the tunnel mean travel time is approximately equal to 0.062 h, suggesting that the time averaged traffic speed through the tunnel is around 32.26 km/h, which agrees well with existing data, suggesting that the three-lane model has the application potential for analyzing the effect of tunnel throttling of vehicular flow and understanding the tunnel bottleneck phenomenon.

In this paper, model equations are presented in Section 2, the numerical method is described in Section 3, numerical results of vehicular flows on freeway with tunnel throttling are discussed in Section 4, and some conclusions are provided in Section 5.

2.   Equations of the three-lane model

In the three lanes Ⅰ, Ⅱ and Ⅲ, for lane number $l\in \left\{1,2,3\right\}$, traffic densities and traffic speeds are labeled by ${\rho }_l$ and $u_l$ respectively, as shown in Fig. 1. Generally, vehicles on lane Ⅰ have the highest free flow speed, and lowest on lane Ⅲ, with a value between the two for vehicles on lane Ⅱ. However, in the tunnel, due to the existence of tunnel throttling, lane Ⅲ is blocked completely and traffic density is equal to jam density, a two-lane continuum model is suitable for vehicular flow on lane Ⅰ and Ⅱ. The road has one initial jam at $x_{\mathrm{A}}$, the tunnel with a length of $L_{\mathrm{t}}$ has an entrance and exit are at $x_{\mathrm{t}1}$ and $x_{\mathrm{t}2}$ respectively. The intersections are at $x_{\mathrm{R}1}$ and $x_{\mathrm{R}2}$, which are connected with lane Ⅲ. In the normal segment, any vehicle attempting to leave the annular road initially makes a lane change and shifts onto lane Ⅲ, except lane-changing happened in the tunnel. It is assumed that lane-changing arises spontaneously to keep the local homogeneity in the perpendicular direction, regardless of whether lane-changing is mandatory or discretionary, except for lane-changing at the point just upstream of the tunnel entrance.

Figure  1.  Illustration of a three-lane vehicular flow with freeway tunnel throttling, as lane Ⅲ in the tunnel is blocked completely (tunnel length $L_{\mathrm{t}}=x_{\mathrm{t}2}-x_{\mathrm{t}1}$).

DownLoad: Full-Size Img PowerPoint

In the three-lane model, traffic densities ${\rho }_l$ and flow rates $q_l={\rho }_l{u}_l$ are taken as the main variables. Let the lane average density be $\rho =\left({\rho }_1+{\rho }_2+{\rho }_3\right)/3$, for vehicles on lane Ⅰ attempting to shift onto lane Ⅱ and Ⅲ, the density is ${\rho }_1-\rho$ in unit of km. Putting the traffic relaxation time on lane $l$ as ${\tau }_l$, labeling the average relaxation time as $\mathit{\tau }=\left({\mathit{\tau }}_1+{\mathit{\tau }}_2+{\mathit{\tau }}_3\right)/3$, if the vehicular lane-changing time is $\tau {\beta }_{*}$, the net lane-changing rate for the governing equation of ${\rho }_1$ can be written as $-\left({\rho }_1-\rho \right)/\left(\mathit{\tau }{\beta }_{*}\right)$. Using random ramp parameter $\sigma$ generated in a small range $\Delta \sigma$ with a median, the equations of the three-lane traffic model may be written as Eq. (1).

where $l_0$ is the length scale of traffic flow, $x_{\mathrm{t}1\mathrm{w}}=x_{\mathrm{t}1}-l_0$ denotes the location of the net lane-changing rate $q_{\mathrm{t}1}$, subscript t represents the tunnel, subscript w denotes the west side of the position $x_{\mathrm{t}1}$, subscript t represents the time derivative, subscript $x$ denotes the spatial derivative of some variables, such as ${\rho }_l$ and $q_l$.

However, for traffic flow in the tunnel, the lane average density is $\rho =\left({\rho }_1+{\rho }_2\right)/2$, for $l\in \left\{1,2\right\}$, the relevant equations are as shown in Eq. (2).

where ${\delta }_{l2}$ and ${\delta }_{l3}$ are respectively the Kronecker deltas.

Eqs. (1), (2) indicate that there is a mass conservation of vehicular motion between lanes Ⅰ, Ⅱ and Ⅲ. Similarly, $R_l$ can be expressed as follows (Bogdanova et al., 2015; Ma et al., 2018; Zhu and Yang, 2013).

where $q_{\mathrm{e}l}$ and $R_l/{\rho }_l$ are equilibrium flow rate and acceleration on lane $l\in \left\{1,2,3\right\}$ respectively, ${\nu }_l$ and ${\tau }_l$ are traffic kinematic viscosity and relaxation time, $p_l$ is traffic pressure which equals to ${\rho }_l{c}_l^2$, and $c_l$ is traffic sound speed.

Adopting $\tau {\beta }_{*}$ to represent lane-changing time, its ratio to relaxation time is given by Eq. (4).

It shows that if the absolute value of traffic densities between the two lanes is less than 1 veh/km, drivers have not attempted to carry out lane-changing so that the ratio ${\beta }_{*}=\infty$; otherwise it is inversely proportional to vehicular spatial headway, equally to unity when traffic flow is at saturation with ${\rho }_{\mathrm{s}}={\rho }_{\mathrm{m}}/\mathrm{e}$. When traffic flow is completely jammed, ${\beta }_{*}=\infty$, indicating that lane-changing is hard to happen for congested flow. For unsaturated traffic flow, ${\beta }_{*}<1$. For instance, at the first critical point on lane Ⅱ, ${\rho }_{*2}=0.0819$ (Table 1), the ratio ${\beta }_{*}=0.15328$, the lane-changing time used at the critical point is about 15% of relaxation time, implying that a driver in free flow needs 1.401 s to change lanes once if the average relaxation time is 9.142 s.

Table  1.  Parameters of vehicular flow on annular freeway.

Parameter	Value	Parameter	Value
vf1 (km/h)	110	${\rho }_{*1}$	0.0736
vf2 (km/h)	100	${\rho }_{*2}$	0.0819
vf3 (km/h)	90	${\rho }_{*3}$	0.0909
vf4 (km/h)	80	${\rho }_{*4}$	0.1021
Xbr1 (m)	73	${\rho }_{\mathrm{c}21}$	0.6525
Xbr2 (m)	65	${\rho }_{\mathrm{c}22}$	0.6374
Xbr3 (m)	58	${\rho }_{\mathrm{c}23}$	0.6190
Xbr4 (m)	51	${\rho }_{\mathrm{c}24}$	0.5985
cτ1	5.147	$x_{\mathrm{R}1}$	40
cτ2	4.879	$x_{\mathrm{R}2}$	60
cτ3	4.582	$x_{\mathrm{A}}$	20
cτ4	4.280	$x_{\mathrm{t}1}$	50
τ1 (s)	7.762	$x_{\mathrm{t}2}$	52
τ2 (s)	9.007	Lt (km)	2
τ3 (s)	10.657	lveh (m)	5.8
τ4 (s)	12.834	uc2 (km/h)	18
ρm (veh/km)	172	Imax	1001
l0 (m)	100	γ	0.382
v0 = ρ*2vf2 (m/s)	2.2756	Δγ	0.05
t0 (s)	43.945	g0 = 1−γ	0.618
L (km)	100
Note: ${\rho }_{*j}$ and ${\rho }_{\mathrm{c}2j}$ are normalized by ${\rho }_{\mathrm{m}}$, tunnel length $L_{\mathrm{t}}=x_{\mathrm{t}2}-x_{\mathrm{t}1}$ , cτ1, cτ2, cτ3, and cτ4 are measured by v0.

 | Show Table

DownLoad: CSV

In comparison with existing modules of lane-changing, the present model is simpler than the behavioral theory reported by Daganzo (2002), which has been used to make predictions for separate groups of lanes while recognizing that the traffic stream is usually composed of aggressive and timid drivers. The simplest version of the theory is found to be qualitatively consistent with experimental observations. However, eight observable parameters are used to specify the simple model.

In the normal road segment excluding the tunnel, lane numbers are $l\in \left\{1,2,3\right\}$, vehicles have different free flow speed and braking distance on different lanes, indicating that equilibrium traffic flow rate is lane-dependent, as shown in Fig. 2. In Fig. 2, $\rho$ is measured by jam density ${\rho }_{\mathrm{m}}$, traffic flow rate has the unit of $q_0={\rho }_{\mathrm{m}}{v}_0$, and $q_{\text{es}j}=c_{\tau j}/\mathrm{e}\left({\rho }_{*j}{v}_{\mathrm{f}j}/{\rho }_{*2}{v}_{\mathrm{f}2}\right),j\in \left\{1,2,3,4\right\}$. Let jam density be ${\rho }_{\mathrm{m}}$, in normal road segment, equilibrium traffic flow rate can be written as proposed by Zhang et al. (2018).

Figure  2.  Fundamental diagrams (FD) for a three-lane vehicular flow.

DownLoad: Full-Size Img PowerPoint

In the tunnel, the lane number is limited to $l\in \left\{1,2\right\}$, as the free flow speed is just the same as tunnel speed limit $v_{\mathrm{f}4}$, equilibrium traffic flow rate is shown in Eq. (6)

For $j\in \left\{1,2,3,4\right\}$, in the definition of the equilibrium traffic speed at saturation state $c_{\tau j}$, the average length of vehicles $l_{\text{veh}}$ has to be used. In the definition of $B_j$, the ratio of $c_{\tau j}$ to the second critical speed $u_{c2}$ on lane $l$, i.e., ${\Lambda }_l$, should be used, as proposed by Zhang et al. (2021).

In particular, $q_{\mathrm{t}1}$ at $x_{\mathrm{t}1\mathrm{w}}$ is the mandatory net lane-changing rate from lane Ⅲ to lane Ⅱ due to the existence of tunnel throttling, the rate is approximated by the random number model based on golden section analysis: the ratio of the mandatory net lane-changing rates to $q_3$ is approximately equal to $\mathit{\gamma }=1-g_0$, here $g_0=0.618$ is the golden section. Hence, let $\mathit{\gamma }$ be a random number with the median $\mathit{\gamma }=0.382$ and the number range $\Delta \mathit{\gamma }=0.05$, the net changing rate at $x_{\mathrm{t}1\mathrm{w}}$ can be written as Eq. (7).

As an example, when $t\in \left(0.2,0.27\right)$ h, the evolution curve of $q_{\mathrm{t}1}$ for initial density normalized by jam density ${\rho }_0=0.29$ can be seen in Fig. 3(a), with Fig. 3(b) showing the random numbers ${\sigma }_1$ and ${\sigma }_2$ for assigning ramp flows at the intersections $x_{\mathrm{R}1}$ and $x_{\mathrm{R}2}$ (Table 1).

Figure  3.  Temporal evolution of $q_{\mathrm{t}1}$, ${\sigma }_1$ and ${\sigma }_2$. (a) Mandatory lane-changing rate $q_{\mathrm{t}1}$ in the unit of ${\rho }_{\mathrm{m}}{v}_0$ for ${\rho }_0=0.29$ when $t\in$(0.2, 0.27) h in the case of RF1. (b) Random numbers for on and off ramp flows at intersections $x_{\mathrm{R}1}$ and $x_{\mathrm{R}2}$.

DownLoad: Full-Size Img PowerPoint

3.   Numerical method

Details of calculation of the numerical flux with the WENO5 scheme (Henrick et al., 2005; Jiang and Shu, 1996) and time derivative term with the RK3 (Shu, 1988; Shu and Osher, 1988) are reported by Zhang et al. (2021). The numerical method WENO5-RK3 is explicit. The vector form of the equations of the continuum model and the condition of numerical stability are presented as below.

In the normal road segment, the pressure gradient $p_{lx}$ is related to sound speed as in Eq. (8).

Using

Instead of $R_l$ for $l\in \left\{1,2,3\right\}$, the governing Eq. (1) can be written as Eq. (10).

where $U={\left({\rho }_1,q_1,{\rho }_2,q_2,{\rho }_3,q_3\right)}^{\mathrm{T}}$, $F\left(U\right)={\left(q_1,q_1^2/{\rho }_1+p_1,q_2,q_2^2/{\rho }_2+p_2,q_3,q_3^2/{\rho }_3+p_3\right)}^{\mathrm{T}}$, and

In the tunnel, $x\in \left[x_{\mathrm{t}1},x_{\mathrm{t}2}\right]$, for $l\in \left\{1,2\right\}$, according to Eq. (2),

Taking $U={\left({\rho }_1,q_1,{\rho }_2,q_2\right)}^{\mathrm{T}}$, $F\left(U\right)={\left(q_1,q_1^2/{\rho }_1+p_1,q_2,q_2^2/{\rho }_2+p_2\right)}^{\mathrm{T}}$, the source term becomes Eq. (13).

The WENO5-RK3 satisfies the Courant-Friedrichs-Lewy (CFL) condition, the Courant number is given by Eq. (14).

where $a_{k,i}$ is the kth eigenvalue of A at $x_i$, $\Delta x$ is the uniform grid length, $I_{\max }$ is the maximum of grid number.

The Courant number CFL (Shui, 1998) is fixed at 0.3 to ensure numerical stability. The main reason for choosing WENO5 rather than other Riemann solvers is that essentially non-oscillatory (ENO) reconstruction (Shu and Osher, 1988) is based on adaptive stencils, such that the optimal stencil is chosen. This provides high-order accuracy and essentially non-oscillatory behavior. WENO reconstruction (Shu, 1988) consists of a convex combination of all the candidate stencils, and constitutes an improvement on ENO schemes on many levels, as reported by Johnsen and Colonius (2006).

4.   Results and discussions

4.1   Simulation parameter

To predict the tunnel throttling effect of annular freeway vehicular flow, numerical simulations are conducted with parameters shown in Table 1. It can be seen that the free flow speeds on lanes Ⅰ, Ⅱ and Ⅲ are $v_{\mathrm{f}1}=110$, $v_{\mathrm{f}2}=100$, and $v_{\mathrm{f}3}=90$ km/h respectively, with the tunnel speed limit $v_{\mathrm{f}4}$ being equal to 80 km/h. With the second critical speed $u_{\mathrm{c}2}=18$ km/h, and the corresponding braking distances X_br for $j\in \left\{1,2,3,4\right\}$, the fundamental diagrams can be determined, as shown by Fig. 2. The second column of Table 1 shows the first and second critical densities ${\rho }_{*j}$ and ${\rho }_{\mathrm{c}2j}$, and positions of the first and second ramp intersections $x_{\mathrm{R}1}$, $x_{\mathrm{R}2}$, the position of initial jam at $x_{\mathrm{A}}$, the tunnel entrance at $x_{\mathrm{t}1}=50$ km, tunnel exit at $x_{\mathrm{t}2}=52$ km, and tunnel length of $L_{\mathrm{t}}=2$ km. The column also shows the average length of cars of $l_{\text{veh}}=5.8$ m, and the second critical speed of $u_{\mathrm{c}2}=18$ km/h.

The third column of Table 1 shows the jam density ${\rho }_{\mathrm{m}}$, the scales of length, speed and time $l_0$, $v_0$ and $t_0$, the maximum number of grid $I_{\max }$ = 1001, total length of the annular freeway $L=\left(I_{\max }-1\right)l_0=100$ km. The median of the random parameter from a golden section analysis $\gamma$ is 0.382, and the relevant range of $\Delta \gamma =0.05$. In the numerical tests, Reynolds number is given by $\text{Re}=l_0{v}_0/\nu =128$. In Table 2, the medians for random numbers, i.e., ${\sigma }_{1\text{av}}$ and ${\sigma }_{2\text{av}}$, and the relevant range $\Delta \sigma$ are shown for the cases LBV, RF0 and RF1, here LBV is the abbreviation of lane blockage vanished. The off and on ramp intersections located respectively at $x_{\mathrm{R}1}$ and $x_{\mathrm{R}2}$.

Table  2.  Parameters of random number generator for ramp flows.

Case	${\sigma }_{1\text{av}}$	${\sigma }_{2\text{av}}$	$\Delta \sigma$
LBV	0.000	0.000	0.00
RF0	0.000	0.000	0.00
RF1	−0.191	−0.191	0.05

 | Show Table

DownLoad: CSV

In particular, it is noted that the average length of cars $l_{\text{veh}}=5.8$ m is just suitable for passenger car, as reported by McShane et al. (1998), but for single unit truck and single unit bus, the length can be changed to 9.1 m and 12.1 m respectively. Indeed, the choice of $l_{\text{veh}}$ could have some influences on simulation results, as traffic pressure $p_l$ and traffic sound speed $c_l$ depend on the parameter $\alpha =l_{\text{veh}}{\rho }_{\mathrm{m}}$, as described by Zhang et al. (2018).

In the numerical simulations, in the normal segment excluding the tunnel, $x\notin \left[x_{\mathrm{t}1},x_{\mathrm{t}2}\right]$, the initial density is assumed to be as Eq. (15).

While in the tunnel, $x\in \left[x_{\mathrm{t}1},x_{\mathrm{t}2}\right]$, it is assumed to be just 38.2% of ${\rho }_0$, such that

with $q_l\left(0,x\right)=q_{\mathrm{e}l}\left(0,x\right)$.

To examine the macroscopic model characterized by the ratio of lane-changing time to relaxation time ${\beta }_{*}$, a numerical study has been carried out by Li et al. (2022) to seek the effects of tunnel speed limit on traffic flow, where the observed speed data (Koshi et al., 1992) and the calculated speed on the basis of a behavioral kinematic wave model developed by Jin (2018) were used to make a comparison, which has shown that the predicted speeds on the basis of a three lane traffic model agree well with published data.

4.2   Threshold of traffic jam formation

As the average vehicle length $l_{\text{veh}}$ is 5.8 m, we choose the lowest contour level as 7 m to determine whether vehicular flow jam has formed. In Fig. 4, spatiotemporal evolution of spatial headway $h_{\mathrm{d}2}$ is shown, from which one can see that there exists a larger $h_{\mathrm{d}2}$ segment that is close to the tunnel end, the length of the segment grows with the increase of time; a lower $h_{\mathrm{d}2}$ segment near the tunnel entrance. Also the initial jam propagates in the downstream direction, and the initial jam has induced several spontaneously jams propagating forward.

Figure  4.  Spatiotemporal evolution of spatial headway $h_{\mathrm{d}2}=$(1−ρ₂)/(ρ_mρ₂). (a) RF0, ${\rho }_0=0.18$. (b) RF0, ${\rho }_0=0.19$. (c) RF1, ${\rho }_0=0.19$. (d) RF1, ${\rho }_0=0.20$.

DownLoad: Full-Size Img PowerPoint

Comparing Fig. 4(a) and (b) and Fig. 4(c) and (d), the density threshold of traffic jam formation ${\rho }_{\text{th}}=0.19$ or 0.20 for RF0 and RF1 (Table 2) are obtained, indicating that the off ramp flow at the ramp intersection at $x_{\mathrm{R}1}=40$ km and the on ramp flow at the intersection at $x_{\mathrm{R}2}=60$ km delay the occurrence of traffic jam slightly.

4.3   Variable distributions

For ${\rho }_0=0.29$, the instantaneous distributions of traffic density ${\rho }_l$ and traffic speed $u_l$, $l\in \left\{1,2,3\right\}$ and density fraction $s_1={\rho }_1/\sum {\rho }_l$ at the time of $t=0.5$ h are shown in Fig. 5. Caused by traffic jam at $x_{\mathrm{t}1}=50$ km, in the segment near the entrance, traffic density ${\rho }_l$ is higher, with lower traffic speed $u_l$. There is a peak of ${\rho }_l$ and a corresponding trough of $u_l$ at a position upstream the initial jam point $x_{\mathrm{A}}=20$ km, suggesting that the tunnel triggered traffic jam propagates in the upstream direction. In the segment near the tunnel exit, ${\rho }_l$ dropped abruptly to a level of 0.1, with small magnitude oscillation at this level, correspondingly $u_l$ rises suddenly to a level of about 0.9, and then oscillates with a small magnitude, caused by the propagation and interaction of traffic waves. When traffic density ${\rho }_l$ is equal to 0.29, the traffic speed $u_l$ has a value around 0.5.

Figure  5.  Variable distributions at t = 0.5 h on the ring road for ρ₀ = 0.29 in the case of RF1. (a) Traffic density. (b) Traffic speed. (c) Density fraction $s_1={\rho }_1/\sum {\rho }_l$.

DownLoad: Full-Size Img PowerPoint

In the tunnel, the density fraction $s_1={\rho }_1/\left({\rho }_1+{\rho }_2\right)$ has a value of around 0.5. However, in the freeway normal segment, $s_1={\rho }_1/\left({\rho }_1+{\rho }_2+{\rho }_3\right)$ has a value around 1/3, just because of the crucial role played by local vehicular homogeneity.

Correspondingly, Table 3 shows the data of ${\rho }_l$, $u_l$ and $s_1$ near the tunnel. It can be seen that in the traffic jam triggered by the tunnel, ${\rho }_l$ is generally over 0.5, excluding the grid on lane Ⅲ at $x=49.90$ km which is nearest to the tunnel entrance at $x_{\mathrm{t}1}=50$ km. In particular, on lanes Ⅰ and Ⅱ, the jam terminates at $x=50.4$ km, as there is a sudden drop of traffic density (${\rho }_1$ or ${\rho }_2$) when $x$ approaches to the adjacent grid at $x=50.5$ km. Downstream in the tunnel segment when the jam terminates, traffic density decreases gradually from a value of around 0.38 to about 0.34, as can be seen in the 2nd and 4th columns of Table 3.

Table  3.  Predicted $\left({\rho }_l,u_l\right)$ for $l\in \left\{1,2,3\right\}$ and $s_1$ near the tunnel at $t=0.5$ h for RF1 and ${\rho }_0=0.29$.

$x$	${\rho }_1$	$u_1$	${\rho }_2$	$u_2$	${\rho }_3$	$u_3$	$s_1$
49.5	0.5474	0.2509	0.5717	0.2140	0.5391	0.2359	0.3301
49.6	0.5476	0.2509	0.5792	0.2055	0.5333	0.2432	0.3298
49.7	0.5476	0.2512	0.5889	0.1941	0.5238	0.2544	0.3298
49.8	0.5466	0.2529	0.6009	0.1800	0.5098	0.2699	0.3298
49.9	0.5418	0.2529	0.6319	0.1852	0.2734	0.4889	0.3744
50.0	0.5634	0.2281	0.5835	0.2204	1.0000	0.0000	0.4912
50.1	0.5520	0.2330	0.5446	0.2362	1.0000	0.0000	0.5034
50.2	0.5242	0.2454	0.5126	0.2509	1.0000	0.0000	0.5056
50.3	0.4957	0.2595	0.4899	0.2626	1.0000	0.0000	0.5030
50.4	0.4809	0.2675	0.4789	0.2679	1.0000	0.0000	0.5010
50.5	0.3846	0.3344	0.3731	0.3448	1.0000	0.0000	0.5076
50.6	0.3717	0.3459	0.3722	0.3456	1.0000	0.0000	0.4997
50.7	0.3704	0.3471	0.3714	0.3463	1.0000	0.0000	0.4993
50.8	0.3691	0.3483	0.3697	0.3478	1.0000	0.0000	0.4996
50.9	0.3676	0.3497	0.3675	0.3498	1.0000	0.0000	0.5001
51.0	0.3655	0.3517	0.3651	0.3520	1.0000	0.0000	0.5002
51.1	0.3632	0.3538	0.3628	0.3541	1.0000	0.0000	0.5003
51.2	0.3610	0.3559	0.3606	0.3562	1.0000	0.0000	0.5002
51.3	0.3588	0.3579	0.3585	0.3582	1.0000	0.0000	0.5002
51.4	0.3567	0.3599	0.3565	0.3601	1.0000	0.0000	0.5002
51.5	0.3547	0.3618	0.3544	0.3621	1.0000	0.0000	0.5002
51.6	0.3527	0.3638	0.3523	0.3641	1.0000	0.0000	0.5003
51.7	0.3507	0.3657	0.3502	0.3662	1.0000	0.0000	0.5004
51.8	0.3485	0.3679	0.3479	0.3685	1.0000	0.0000	0.5004
51.9	0.3463	0.3700	0.3456	0.3706	1.0000	0.0000	0.5005
52.0	0.3438	0.3725	0.3431	0.3732	1.0000	0.0000	0.5005
52.1	0.2350	0.4611	0.2375	0.4549	0.0684	0.5235	0.4345
52.2	0.1773	0.5494	0.1806	0.5280	0.1214	0.5781	0.3699
52.3	0.1584	0.6095	0.1587	0.5860	0.1413	0.5775	0.3456
52.4	0.1368	0.6724	0.1362	0.6461	0.1278	0.6388	0.3413
52.5	0.1196	0.7320	0.1204	0.7006	0.1147	0.6768	0.3372
52.6	0.1108	0.7769	0.1140	0.7361	0.1077	0.7115	0.3333
Note: ul (l = 1, 2, 3) is normalized by vf2.

 | Show Table

DownLoad: CSV

Downstream of the tunnel end $x_{\mathrm{t}2}=52$ km, with $x$ increasing from 52.1 to 52.6 km, ${\rho }_1$ drops from 0.2350 to 0.1108, ${\rho }_2$ drops from 0.2375 to 0.1140; while ${\rho }_3$ increases from 0.0684 to 0.1413 at $x=52.3$ km at first and then decreases gradually to 0.1077.

4.4   Travel time

In this study, travel time is predicted using grid traffic speed as previously reported by Zhang et al. (2018), which is different from the work of Chang and Mahmassani (1988) and Wang et al. (2016). It is noted that in the tunnel lane Ⅲ $x\in \left[x_{\mathrm{t}1},x_{\mathrm{t}2}\right]$, traffic speed is zero, which is not appropriate for the prediction of travel time through lane Ⅲ using grid traffic speed. Alternatively, the density-averaged grid traffic speed, i.e., $\left(q_1+q_2\right)/\left({\rho }_1+{\rho }_2\right)$ is used, as the tunnel length is just 2% of the total road length.

In this paper, it is found that in the case of LBV (or the case of three lane tunnel), as shown by the coarse solid purple curve in Fig. 6(a), the mean travel time through lane Ⅱ $T_{\mathrm{t},2\text{av}}$ is slightly higher than that predicted for the cases RF0 and RF1, implying that tunnel throttling only has a slight influence on the mean travel time.

Figure  6.  Distributions of travel time with ρ₀. (a) Mean travel time $T_{\mathrm{t},2\text{av}}$. (b) Tunnel mean travel time $T_{\text{tu},2\text{av}}$.

DownLoad: Full-Size Img PowerPoint

$T_{\mathrm{t},2\text{av}}$ for the case RF0 is illustrated by the blue solid curve with circles, as shown in Fig. 6(a), with the corresponding data given in the 3rd column of Table 4. $T_{\mathrm{t},2\text{av}}$ grows with the increase of initial density ${\rho }_0$. When ${\rho }_0=0.07$, $T_{\mathrm{t},2\text{av}}=1.01$ h, which is almost equal to the mean travel time calculated directly with the free flow speed $v_{\mathrm{f}2}$. When ${\rho }_0$ increases from the second threshold of jam formation 0.19 to the saturation density of vehicular flow ${\rho }_{\mathrm{s}}=1/\mathrm{e}\approx 0.368$, the mean travel time $T_{\mathrm{t},2\text{av}}$ increases from 1.482 to 2.496 h. For ${\rho }_0=0.37$, at over saturation, the mean travel time $T_{\mathrm{t},2\text{av}}$ is 2.507 h. The green deltas represent the mean travel time $T_{\mathrm{t},2\text{av}}$ for the case of RF1, which almost overlap the circles for the case of RF0, indicating that the ramp flow influences on the mean travel time is very small.

Table  4.  Distributions of T_{t, lav}, T_{tu, lav} and $T_{\mathrm{t},l}^{\prime }$ for RF0.

${\rho }_0$	$T_{\mathrm{t},1\text{av}}$ (h)	$T_{\mathrm{t},2\text{av}}$ (h)	$T_{\mathrm{t},3\text{av}}$ (h)	$T_{\text{tu},1\text{av}}$ (h)	$T_{\text{tu},2\text{av}}$ (h)	$T_{\text{tu},3\text{av}}$ (h)	$T_{\mathrm{t},1}^{\prime }$ (h)	$T_{\mathrm{t},2}^{\prime }$ (h)	$T_{\mathrm{t},3}^{\prime }$ (h)
0.070	0.924	1.010	1.120	0.024	0.025	0.025	0.003	0.002	0.002
0.150	1.233	1.305	1.372	0.044	0.045	0.044	0.022	0.030	0.022
0.190	1.399	1.482	1.550	0.060	0.060	0.060	0.034	0.044	0.037
0.200	1.439	1.524	1.593	0.061	0.061	0.061	0.038	0.047	0.041
0.210	1.484	1.574	1.641	0.062	0.062	0.062	0.041	0.050	0.045
0.368	2.344	2.496	2.595	0.063	0.062	0.062	0.030	0.036	0.034
0.370	2.354	2.507	2.607	0.063	0.062	0.062	0.031	0.038	0.035

 | Show Table

DownLoad: CSV

In Fig. 6(b), the tunnel mean travel time through lane Ⅱ $T_{\text{tu},2\text{av}}$ is plotted as a function of initial density ${\rho }_0$, where the blue solid cure with circles show the tunnel mean travel time through lane Ⅱ $T_{\text{tu},2\text{av}}$, which is consistent with the data given by the 6th column of Table 4, the green deltas represent $T_{\text{tu},2\text{av}}$ predicted for the case of RF1 with ramp flow effect, while the coarse solid purple curve shows $T_{\text{tu},2\text{av}}$ for the case of LBV. For the cases of RF0, when ${\rho }_0$ passes through the turning point at ${\rho }_{\text{th}}=0.19$, the mean travel time exhibits a slowly growing plateau that ends at the point ${\rho }_0=0.37$. As shown in Fig. 6(b), when ${\rho }_0$ is lower than the threshold ${\rho }_{\text{th}}=0.19$, $T_{\text{tu},2\text{av}}$ for the case of RF1 is almost the same as that calculated for the case RF0. As in the case of RF1, the threshold of traffic jam formation is slightly delayed to 0.20, as shown in Fig. 4, indicating that the ramp flow effect on $T_{\text{tu},2\text{av}}$ is also very small. However, for the case of LBV, the turning point occurs at 0.22, indicating that tunnel throttling results in a smaller density threshold of traffic jam formation.

As shown in the 6th column of Table 4, the platform height is about 0.062 h, implying that as soon as a traffic jam appears and propagates in the upstream direction, the time-averaged traffic speed through the tunnel $\left(L_{\mathrm{t}}/T_{\text{tu},2\text{av}}\right)$ is around 32.26 km/h, which agrees well with the time averaged speed of 28.9 km/h from observed speed data (Koshi et al., 1992) and the time averaged speed of 33.6 km/h calculated on the basis of a behavioral kinematic wave model (Jin, 2018).

In Fig. 7, the mean travel time $T_{\mathrm{t},l\text{av}}$, root mean square (RMS) of travel time $T_{\mathrm{t},l}^{\prime }$, tunnel mean travel time $T_{\text{tu},l\text{av}}$, and its root mean square $T_{\text{tu},l}^{\prime }$ are plotted as functions of initial density ${\rho }_0$.

Figure  7.  Distributions of travel time and root mean square with ρ₀. (a) Mean travel time $T_{\mathrm{t},l\text{av}}$. (b) RMS of travel time $T_{\mathrm{t},l}^{\prime }$. (c) Tunnel mean travel time $T_{\text{tu},l\text{av}}$. (d) RMS of tunnel travel time $T_{\text{tu},l}^{\prime }$.

DownLoad: Full-Size Img PowerPoint

For the case of RF0, $T_{\mathrm{t},l\text{av}}$ and $T_{\text{tu},l\text{av}}$ for $l=1,2,3$ are illustrated by the black deltas, green circles, and blue gradients respectively. While for the case of RF1, the ramp parameter has a median of 0.191 (Table 2) with a range of 0.05, $T_{\mathrm{t},l}^{\prime }$ and $T_{\text{tu},l}^{\prime }$ for $l=1,2,3$ are shown by black, green and blue curves respectively. It can be seen that ramp flow has brought a very small influence on $T_{\mathrm{t},l\text{av}}$, but an observable small influence on $T_{\mathrm{t},l}^{\prime }$, usually causing a smaller value of $T_{\mathrm{t},l}^{\prime }$ for a given initial density, such an effect becoming more acute when the initial density is beyond the threshold ${\rho }_{\text{th}}$.

As the free flow speed $v_{\mathrm{f}l}$ determines equilibrium traffic speed on lane $l$, i.e., $q_{\mathrm{e}l}/{\rho }_l$, with the value of $v_{\mathrm{f}l}$ given in the first column of Table 1, for a given initial density ${\rho }_0$, it is reasonable that $T_{\mathrm{t},3\text{av}}$ takes a value equal to the largest among the three mean travel times, as shown in Fig. 7(a). However, those values are all lower than that predicted for the case of LBV, as shown by the coarse solid purple curve.

In Fig. 7(b)–(d), it can be seen that the coarse solid purple curve denoting the corresponding variable for $l=3$ in the case of LBV, deviates clearly from the gradient symbols, suggesting that tunnel throttling has brought a significant effect on the RMS of travel time, tunnel mean travel time as well as the relevant RMS value when the initial density is below the threshold.

When traffic jam originated by the tunnel appears at the tunnel entrance, there is a rarefaction wave propagating in the downstream direction, which decreases the responsiveness of grid traffic speed in the tunnel to the variation of initial density ${\rho }_0$. As a result, the fluctuation of travel time has a peak near the threshold ${\rho }_{\text{th}}$ (Fig. 7(b)), the peak value is usually below 0.05 h; the tunnel mean travel time has a plateau with a height of about 0.062 h (Fig. 7(c)). For the case of LBV, the fluctuation of tunnel travel time also occurs a peak at the density threshold of 0.22, the peak is around 0.008 h, as can be seen in Fig. 7(d).

4.5   Vehicle fuel consumption

To predict vehicle fuel consumption by interpolation, time averaged grid traffic speed is used with a vehicular performance curve as shown in Fig. 8. The performance curves for lane Ⅰ, Ⅱ or Ⅲ have steps, reflecting the dependence of vehicle fuel consumption fc on vehicular speed $u$.

Figure  8.  Distribution of fuel consumption fc as a function of vehicular speed (the volume unit 1 L = 1000 mL, and the vehicular speed is in the unit of $v_{\mathrm{f}2}$).

DownLoad: Full-Size Img PowerPoint

According to the three vehicle performance curves, with the time averaged grid traffic speed ${\overline{u}}_l$, the vehicle fuel consumption through the grid length $\Delta x_i=l_0$ for $i\in \left[1,I_{\max }\right]$, i.e., ${\text{fc}}_l$ can be estimated by linear interpolation. As $l_0$ is assigned as 100 m, the unit of fc is L/100 km. For the convenience of illustration, mL is selected as the unit of the vehicle grid fuel consumption.

For ${\rho }_0=0.190,0.250\text{and}0.368$, the distributions of ${\overline{u}}_l$ and vehicle grid fuel consumption ${\text{fc}}_l$ are shown in Fig. 9. It can be seen that the time averaged grid traffic speed ${\overline{u}}_l$ has a trough at the tunnel entrance at $x_{\mathrm{t}1}=50$ km. As illustrated by the purple solid curve, the off-ramp flow at $x_{\mathrm{R}1}=40$ km results in an abrupt rise of ${\overline{u}}_l$ for $l=1,2$ to a peak then decreases gradually in the downstream segment near $x_{\mathrm{R}1}$, where ${\overline{u}}_3$ has an obvious peak for ${\rho }_0=0.368$. Due to the on-ramp flow at $x_{\mathrm{R}2}=60$ km, ${\overline{u}}_3$ also has a trough in the downstream segment near $x_{\mathrm{R}2}$.

Figure  9.  Distributions of time averaged grid traffic speed ${\overline{u}}_1,{\overline{u}}_2,{\overline{u}}_3$ and fuel consumption through a grid length fc₁, fc₂, fc₃. (a) ${\overline{u}}_1$ at ${\rho }_0=0.19$. (b) fc₁ at ${\rho }_0=0.19$. (c) ${\overline{u}}_2$ at ${\rho }_0=0.25$. (d) fc₂ at ${\rho }_0=0.25$. (e) ${\overline{u}}_3$ at ${\rho }_0=0.368$. (f) fc₃ at ${\rho }_0=0.368$.

DownLoad: Full-Size Img PowerPoint

The right-hand side of Fig. 9 indicates that there are corresponding peaks for the troughs of ${\overline{u}}_l$. In particular, for ${\rho }_0=0.368$, being relevant to the effect of initial jam, a peak of ${\text{fc}}_3$ appears at $x_{\mathrm{A}}$, the black solid curve for RF1 deviates from the green circles for RF0 in the downstream segment near $x_{\mathrm{R}1}$.

Taking the sum of fc_l(x_i), the total vehicle fuel consumption through the annular freeway can be obtained as Eq. (17).

where the factor ${10}^{-3}$ is used to change the unit from mL to L.

Being consistent with the data given in Table 5, the vehicle fuel consumption through the freeway ring ${\text{Fu}}_l$ is plotted as a function of initial density ${\rho }_0$, as shown in Fig. 10(a), where coarse solid curves are obtained in the case of LBV, with circles and squares corresponding to the cases of RF0 and RF1 respectively. The coarse solid curves are shown in order to demonstrate the tunnel throttling of vehicular flow more clearly. ${\text{Fu}}_l$ is lane dependent, and distributed in the range of ${\rho }_0\in \left[0.07,0.37\right]$ concavely, implying that there exists a local minimum. Fig. 10(a) shows that in the range of ${\rho }_0\in \left[0.07,0.37\right]$, ${\text{Fu}}_l$ is below 8.0 L.

Table  5.  Distributions of ${\text{Fu}}_l$ for LBV, RF0 and RF1.

${\rho }_0$	LBV				RF0				RF1
	${\text{Fu}}_1\left(\mathrm{L}\right)$	${\text{Fu}}_2\left(\mathrm{L}\right)$	${\text{Fu}}_3\left(\mathrm{L}\right)$		${\text{Fu}}_1\left(\mathrm{L}\right)$	${\text{Fu}}_2\left(\mathrm{L}\right)$	${\text{Fu}}_3\left(\mathrm{L}\right)$		${\text{Fu}}_1\left(\mathrm{L}\right)$	${\text{Fu}}_2\left(\mathrm{L}\right)$	${\text{Fu}}_3\left(\mathrm{L}\right)$
0.070	5.965	6.970	7.959		5.974	6.987	7.968		5.975	6.987	7.968
0.080	5.911	6.908	7.930		5.937	6.950	7.952		5.938	6.952	7.953
0.090	5.848	6.829	7.897		5.895	6.880	7.937		5.895	6.881	7.938
0.190	5.572	6.397	7.189		5.656	6.505	7.316		5.644	6.490	7.306
0.200	5.557	6.392	7.138		5.642	6.499	7.274		5.633	6.484	7.265
0.210	5.567	6.401	7.106		5.638	6.488	7.236		5.627	6.480	7.230
0.260	5.724	6.410	7.061		5.765	6.471	7.166		5.746	6.460	7.152
0.270	6.209	6.420	7.062		6.181	6.479	7.160		6.133	6.468	7.145
0.280	6.264	6.439	7.070		6.214	6.491	7.163		6.168	6.479	7.148
0.300	6.327	6.481	7.086		6.264	6.521	7.166		6.246	6.507	7.156
0.330	6.433	6.573	7.153		6.377	6.613	7.228		6.385	6.588	7.206
0.360	6.560	7.067	7.260		6.500	7.043	7.326		6.490	7.001	7.280
0.368	6.596	7.098	7.291		6.535	7.081	7.354		6.516	7.027	7.291
0.370	6.607	7.106	7.292		6.531	7.081	7.347		6.510	7.030	7.283

 | Show Table

DownLoad: CSV

Figure  10.  Initial density dependents of the variables. (a) The fuel consumption ${\text{Fu}}_l$. (b) The additional fuel consumption $\delta {\text{Fu}}_l$.

DownLoad: Full-Size Img PowerPoint

Comparing the fuel consumption illustrated by circles and squares for the cases RF0 and RF1, it can be seen that ramp flow merely results in an observable small deviation of ${\text{Fu}}_l$ when ${\rho }_0>0.27$.

To show the tunnel throttling effect on fuel consumption through the annular freeway more clearly, the difference of fuel consumption to that consumed in the case of LBV called as the additional fuel consumption is calculated by Eq. (18).

As shown in Fig. 10(b), the difference $\delta {\text{Fu}}_l$ is positive for $l=3$, but negative only when initial density ${\rho }_0$ is above 0.35 for $l=2$, or above 0.26 for $l=1$.

Examining the distributions illustrated in Fig. 10(b), in the cases of RF0 and RF1, if ${\rho }_0$ is not over 0.368, $\delta {\text{Fu}}_3$ is positive, with a local maximum around 0.13 L $\delta {\text{Fu}}_2$ changes from positive to negative at ${\rho }_0=0.35$ in the case of RF1 as shown by the blue gradients, but the change happens at ${\rho }_0=0.345$ in the case of RF1 as illustrated by the green filled circles. While both $\delta {\text{Fu}}_1$ change to negative at ${\rho }_0=0.27$ as shown by the red deltas. In the case of RF0, $\delta {\text{Fu}}_3$ is above 0.05 L for the range of ${\rho }_0\in \left[0.1,0.36\right]$, but $\delta {\text{Fu}}_2$ is above 0.05 L merely for a narrowed range of ${\rho }_0\in \left[0.09,0.28\right]$.

5.   Conclusions

A three-lane continuum model is developed to predict the effect of tunnel throttling on annular freeway vehicular flow. Based on the continuum model, numerical simulations with a reliable method of 3rd-order accuracy are conducted, with the following conclusions.

(1) The three-lane continuum model is characterized by the vehicular lane-changing time model to describe net lane-changing rate between adjacent lanes, the model of random number generated in a small range around a median from a golden section analysis, is proposed to describe the mandatory lane-changing rate just upstream of the tunnel having two lanes. The three-lane model has the application potential for analyzing the effect of tunnel throttling of vehicular flow and understanding the tunnel bottleneck phenomenon.

(2) Tunnel throttling leads to an earlier traffic jam formation in comparison with the case without tunnel throttling. Under the conditions adopted in this study, the density threshold of traffic jam formation in unit of jam density is around 0.19, while for the case without tunnel throttling the threshold is 0.22. The ramp effect slightly delays the occurrence of traffic jam, making the threshold become 0.20.

(3) It is found the mean travel time for the case without tunnel throttling is slightly longer than that for the case with tunnel throttling. If the tunnel has originated a traffic jam at the tunnel entrance, the tunnel mean travel time is approximately equal to 0.062 h, suggesting that the time averaged traffic speed through the tunnel is around 32.26 m/h, which agrees well with existing data.

(4) The time averaged traffic speed can be used to estimate travel time and vehicle fuel consumption through every lane. The vehicle fuel consumption through each lane is lane dependent, can be estimated by interpolation with vehicle performance curve. The vehicle fuel consumption varies concavely with initial density. Under the conditions of in this paper, the vehicle fuel consumption is in the range of 5.56–8.00 L. As a counterpart of comparison, for the case of lane blockage vanished without ramp flow effect, the additional fuel consumption for vehicles through lane Ⅲ is above 0.05 L, when initial density is in the range from 0.10 to 0.36; but for vehicles through lane Ⅱ, the additional fuel consumption is above 0.05 L only when initial density is in the range of 0.09–0.28.